Équilibre d'un solide soumis à 2 ou 3 forces

Un solide est en équilibre si tous ses points sont au repos (il ne bouge pas)

Équilibre d'un solide soumis à 2 forces

 Prenons un solide (S) assez léger (vous allez comprendre pourquoi!) comme une plaque de carton:

Nous la soumettons à 2 forces:

Pour pouvoir représenter ces forces, il nous manque leur intensité respective:

Pour cela, on remplace les mains par des dynamomètres:

Qu'observe-t-on?

et ont la même intensité: 3 N.  On peut maintenant faire la représentation des forces:

Loi d'équilibre de 2 forces:

Et donc:

Pourquoi a-t-on faite cette étude sur une plaque légère?  

C'est tout simplement pour négliger son poids par rapport aux 2 autres forces. Si son poids n'avait pas été négligé, on aurait eu affaire à trois forces:

Équilibre d'un solide soumis à 3 forces (non parallèles)

Étudions le cas classique d'un objet soumis à trois forces non parallèle:

Un objet (S) est suspendu à deux fils comme indiqué sur le schéma:

A quelles forces est soumis le solide S?

- à la force exercée par ma main droite;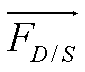

- à la force exercée par la main gauche ;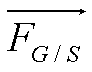

- et à son propre poids .

De la même manière que dans le cas de 2 forces vu plus haut, pour mesurer F_D/S et F_G/S, il suffit de suspendre de la même manière l'objet S à deux dynamomètres.

Pour mesurer l'intensité P du poids de S, il suffit de le suspendre (seul!) à un dynamomètre.

Après avoir fait ces mesures, on peut réaliser le schéma suivant et remplir le tableaux de caractéristiques:

Nom de la force Droite d'action Sens   point d'application A B G Intensité 1,5 N 1 N 2 N

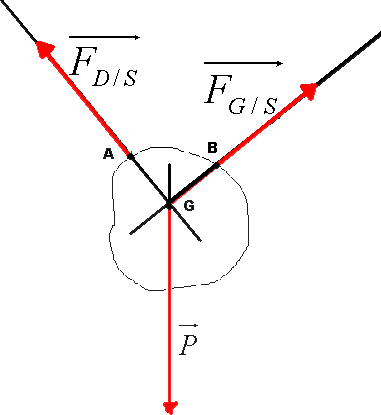Nous pouvons déjà faire une première remarque:

Les 3 droites d'action sont concourantes (elles passent par un seul point)

Maintenant nous allons faire une construction géométrique appelée dynamique des forces:

Cela est très simple: il suffit de mettre les forces bout à bout: 

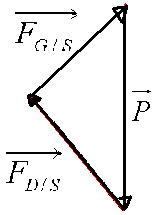on commence par une force	, puis, au bout de celle-ci on y adjoint une deuxième	et enfin on applique la dernière qu'il reste à placer (le tout en respectant les sens et directions)

Et on remarque que la dynamique des forces est fermée

On dit que la somme des forces est nulle est on note:

Loi d'équilibre de 3 forces:

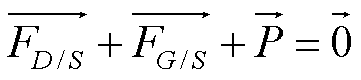
Si un solide est en équilibre sous l'actions de 3 forces; et alors: - Les trois droites d'actions sont concourantes - Leur dynamique des forces est fermé:

Et donc: