1) L'écriture des nombres:

    Pour écrire un nombre en toute lettre, nous avons besoin de connaître 26 mots:

zéro, un, deux, trois, quatre, cinq, six, sept, huit, neuf, dix, onze, douze, treize, quatorze, quinze, seize;

vingt, trente, quarante, cinquante, soixante;

cent, mille, million, milliard.

    Pour écrire un nombre en chiffre, il faut regrouper les chiffres 3 par trois 3 en allant:

- de la droite vers la gauche pour les chiffres avant la virgule;

- de la gauche vers la droite pour les chiffres après la virgule.

Tableau de numération:

Nous allons lire et écrire en toutes lettres le nombre suivant:

12 452 630 781,125

On complète le tableau en partant de la virgule (entre unité et dixièmes)

milliards			millions			milliers			unité
	1	2	4	5	2	6	3	0	7	8	1,	1	2	5

Nous lisons donc:

douze milliard quatre cent cinquante deux million six cent trente mille sept cent quatre vingt un et cent vingt cinq millièmes.

remarque: il est inutile de préciser "unité".

2) les nombres décimaux

Définition:

Un nombre décimal est un nombre:

- qui s'écrit, ou qui peut s'écrire avec une virgule;

- qui est totalement connu.

Exemples: Avec la calculette vous obtenez:

7 ÷ 4 = 1,75          7 ÷ 3 = 2,333333333333333.................      3÷2 = 1,5

1,75 et 1,5 sont des nombres décimaux car il s'écrivent avec une virgule et ils sont totalement connus.

3 est un nombre décimal car il peut s'écrire 3,0 (donc avec une virgule) et il est totalement connu.

En revanche le résultat de 7÷3 n'est pas un nombre décimal car il n'est pas totalement connu (en fait il y a une infinité de 3 après la virgule)

12 est la partie entière de 12,236

0,236 est la partie décimale de 12,236

Écritures particulières:

les nombres plus petits que 1:

un dixième = 1÷10 = 0,1

Imaginons une règle de 1m de long que vous coupez en 10 morceaux de mêmes longueurs: vous obtenez alors un dixième de mètre = 0,1 m (en fait 10 cm)

un centième = 1÷100 = 0,01

un millième = 1÷1000 = 0,001    etc.............

On emploie souvent une notation scientifique:

0,1 = 10^-1    ;    0,01 = 10^-2    ;    0,001 = 10^-3 ............

3) Comparaison des nombres décimaux

Comparer 2 nombres, c'est dire lequel est le plus grand (ou le plus petit) ou dire s'ils sont égaux.

On utilise les signes: < ; = et >

Exemple: 

2<3 signifie: 2 est plus petit que 3    ( "la pointe du signe < pique le plus petit")

5>0 signifie : 5 est plus grand que 0

On peut donc écrire: 4<7 ou 7>4

Nous allons classer les nombres { 5  ;  4,9  ;   5,82  ; 5,802 }

du plus petit au plus grand (ordre croissant )

puis du plus grand au plus petit (ordre décroissant)

1ère étape: on compare les parties entières des nombres (ici 4 et 5)

donc 4,9 (partie entière 4) est plus petit que 5  ;  5,82  ;  5,802  (partie entière 5)

Il reste à comparer 5 ; 5,82 et 5,802

2ème étape: 

Pour les nombres qui ont la même partie entière, on peut ajouter des zéros à la fin de la partie décimale pour qu'ils aient tous le même nombre de chiffre après la virgule:

5 --->  5,000                 5,82 ---> 5,820              5,802 reste comme il est.

3ème étape: On range les parties décimales par ordre croissant 

000 < 802 < 820      donc    5,000 <  5,802 < 5,820

et on supprime les zéros inutiles:

Par ordre croissant:  4,9<5<5,802 < 5,82  et donc par ordre décroissant :  5,82 > 5,802 > 5 > 4,9

Encadrer un nombre:

Plaçons le nombre 2,6 sur un axe gradué:

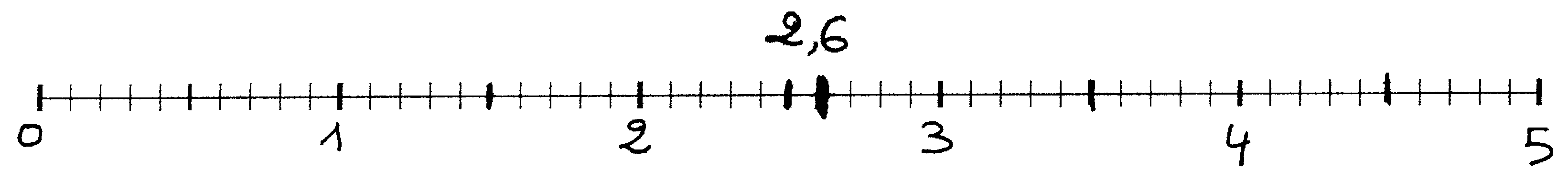Nous voyons que 2,6 est compris entre les entiers 2 et 3

2<2,6 et 2,6<3 on écrit alors 2 < 2,6 < 3

Nous avons encadré 2,6 et  2 < 2,6 < 3 est un encadrement de 2,6.

Nous aurions pu tout aussi bien écrire:2,5 < 2,6 < 4 qui est aussi un encadrement de 2,6.(Il y a une infinité de façon d'encadrer un nombre!)

4) arrondis.

Dans la vie quotidienne ou au travail, il est souvent inutile de connaître des valeurs trop précisément. Par exemple, lorsque nous nous pesons le pèse personne nous indique 65,6 kg alors qu'en réalité c'est peut être  65,59214....kg, mais une telle précision nous est inutile.

Inversement, les joailliers pèsent leurs pierres au milligramme près et sur certaines pièces métalliques, le tourneur doit travailler avec précision.  

On peut encadrer par deux nombres entiers consécutifs (qui se suivent): 2,6 est encadré par 2 et 3.

3 < 3,4 < 4

3,4 est plus proche de 3 que de 4, on dit alors que 3 est l'arrondi à l'unité de 3,4.

Arrondir un nombre à l'unité, c'est prendre le nombre entier le plus proche de ce nombre.

On peut encadrer par deux nombres décimaux successifs qui n'ont qu'un chiffre après la virgule.

5,7 < 5,78 < 5,8 est un encadrement au dixième de 5,78

Ajoutons des zéros: 5,70 < 5,78 <5,80

78 est plus proche de 80 que de 70, 

5,8 est donc l'arrondi au dixième de 5,78.

De la même manière, on peut arrondir au millième, au dix millièmes etc....

Une règle simple:

Si le nombre à arrondir fini par 0; 1; 2 ; 3 ; 4 on "arrondit en dessous"

exemple: l'arrondi au millième de 0,164 7 est: 0,164 (0,164<0,164 7<0,165)

Si le nombre à arrondir fini par 5; 6; 7 ; 8 ; 9 on "arrondit au dessus"

exemple: l'arrondi au centième de 8,066 est: 8,07 (8,06<8,066<8,07)