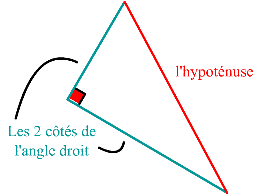
Un triangle rectangle est un triangle possédant un angle droit.
Le côté le plus long s'appelle l'hypoténuse du triangle
La propriété de Pythagore
| - Calculer une mesure de côté de
triangle rectangle avec la propriété de Pythagore
- Identifier un triangle rectangle |
|
Un triangle rectangle est un triangle possédant un angle droit. Le côté le plus long s'appelle l'hypoténuse du triangle |
|
| [AC]
et [BC] sont les deux côtés de l'angle droit.
[AB] est
l'hypoténuse du triangle |
|
Ainsi, dans un triangle rectangle, si on connaît les longueurs de 2 côtés quelconques on doit connaître la longueur du 3ième côté.
Autrement dit: il existe une relation entre les 3 côtés d'un triangle rectangle.
C'est un mathématicien et philosophe grec , Pythagore (570 - 500 avant J.C.) qui a laissé son nom à cette relation. Mais en fait, les Babyloniens la connaissait déjà depuis 1000 ans.
|
Propriété de Pythagore: Dans un triangle rectangle:
(rappel: AB² = AB x AB) |
D'après la propriété de Pythagore: Si ABC est un triangle rectangle en C alors : AB² = AC² + BC² |
Vérifions sur un triangle rectangle quelconque dont on a mesuré les longueurs des côtés à la règle:
|
longueurs en cm |
BC² = 7,5² = 56,25
AC² + AB² = 6² + 4,5² AC² + BC² = 36 + 20,25 = 56,25 on a bien: BC² = AC² + BC² (sacré Pythagore!!) (ne pas oublier de mettre toutes les longueurs dans la même unité pour appliquer la relation de Pythagore) |
|
Ici, saisissez la longueur de deux côtés quelconques.....et vous aurez la longueur du troisième: |
Maintenant que nous avons la relation, nous allons nous en servir: connaissant la longueur de 2 côtés d'un triangle rectangle,
nous allons calculer la longueur du troisième:
| Dans le triangle rectangle ci-contre, calculons la longueur
manquante:
1) Écrire la propriété de Pythagore: Le triangle MNP étant rectangle en P, d'après la relation de Pythagore: MN² = NP² + MP² 2) On remplace, dans la relation, les longueurs connues par leur valeur: MN² = 4,8² + 3,6 ² MN² = 23,04 + 12,96 donc MN² = 36 3) On résout l'équation qui en résulte:
d'où MN = 6 cm |
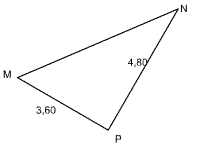
cotes en cm
|
| Dans le triangle rectangle
ci-contre, calculons la longueur manquante:
1) Écrire la propriété de Pythagore: Le triangle ABC étant rectangle en A, d'après la relation de Pythagore: BC² = AB² + AC² 2) On remplace, dans la relation, les longueurs connues par leur valeur: 6,5² = 5,2² + AC ² 42,25 = 27,04 + AC ² 3) On résout l'équation qui en résulte: 42,25 = 27,04 + AC ² donc AC² = 42,25 - 27,04 c'est à dire: AC² = 15,21 d'où d'où AC = 3,9 m |
|
Si un triangle est rectangle, alors on peut appliquer la relation de Pythagore.
|
Inversement: Si les longueurs des côtés d'un triangle vérifie la propriété de Pythagore alors celui-ci est rectangle. |
Soit ABC un triangle:
si BC² = AC² + AB² alors ABC est un triangle rectangle (en A) (ne pas oublier de mettre toutes les longueurs dans la même unité pour appliquer la relation de Pythagore) |
Exemples:
Soit un triangle dont les longueurs des côtés sont: AB = 18 mm ; AC = 30 mm et BC = 24 mm.
Ce triangle est-il rectangle?
| Il suffit de faire la somme des carrés des 2 plus petites longueurs (AB et BC) | AB² + BC² = 18² + 24²
AB² + BC² = 324 + 576 AB² + BC² = 900 |
| Et de comparer avec le carré de la longueur du plus grand côté (AC): | AC² = 30² = 900
On a donc AB² + BC² = AC² |
ABC est donc un triangle rectangle. Son hypoténuse
est [AC] (le
plus long côté) et l'angle droit est donc l'angle ![]() (car A et C sont les deux extrémités de l'hypoténuse)
(car A et C sont les deux extrémités de l'hypoténuse)
Soit un triangle dont les longueurs des côtés sont: AB = 5 m ; AC = 6 m et BC = 7,5 m.
Ce triangle est-il rectangle?
De la même manière que précédemment:
Somme des carrés des 2 plus petites longueurs:
AB² + AC² = 5² + 6² = 25 + 36 = 61
BC² = 7,5² = 56,25
C'est à dire: AB² + AC² ¹
ABC n'est donc pas un triangle rectangle.