| Un quadrilatère est une figure à 4 côtés. |  |
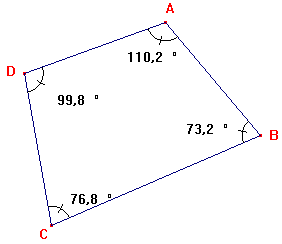
| Propriété: La somme des angles
intérieurs d'un quadrilatère est égale à 360°
Ici:
|
 |
Les quadrilatères
| Un quadrilatère est une figure à 4 côtés. |  |
| Propriété: La somme des angles
intérieurs d'un quadrilatère est égale à 360°
Ici:
|
 |
Les quadrilatères particuliers
Le trapèze:
| Un trapèze est un quadrilatère dont 2 côtés sont parallèles | 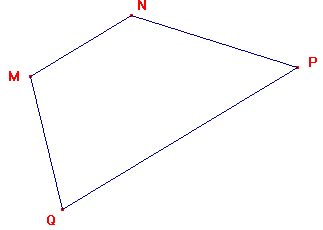 |
| Vocabulaire:
Des 2 côtés parallèles: le plus grand s'appelle: la grande base le plus petit s'appelle: la petite base La distance entre les deux droites supportant ces côtés s'appelle la hauteur du trapèze |
|
Le parallélogramme
| Un parallélogramme est un quadrilatère dont
les côtés opposée sont parallèles 2 à 2:
Ici: ABCD est un parallélogramme: (AB) |
 |
| Propriétés: | |
| Dans
un parallélogramme, les côtés opposés ont la même longueur.
ici: AB=DC et AB=DC |
 |
| Dans
un parallélogramme, les diagonales se coupent en leur milieu.
ici: les diagonales (AC) et (BD) se coupent en O. O est le milieu de [AC] et de [BD] |
 |
Construction d'un parallélogramme:
Avant de procéder à la construction d'un parallélogramme, il faut connaitre cette étape important:
compléter un parallélogramme connaissant 2 côtés consécutifs:
le losange
| Un losange est un quadrilatère ayant ses
côtés égaux et parallèles 2 à 2 égaux
Un losange est donc un parallélogramme particulier. |
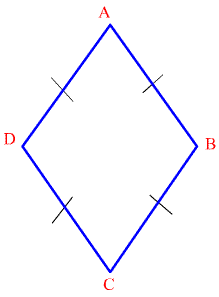 |
| Les diagonales d'un losange sont perpendiculaires |  |
le rectangle
| Un rectangle est un
parallélogramme ayant un angle droit.
Il a donc en fait 4 angles droits. |
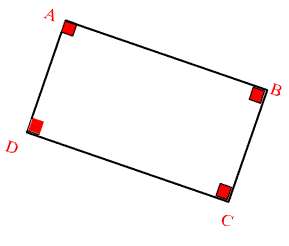 |
| Les diagonales d'un rectangle ont la même longueur et elles se coupent en leur milieu O. Ce milieu est centre du cercle circonscrit au rectangle. |  |
le carré
| Un carré est ,à la fois, un rectangle et un losange |  |
| Les diagonales d'un carré sont:
- perpendiculaires; -de même longueur ; - se coupent en leur milieu; - ce point de concours est le centre du cercle inscrit et circonscrit au carré. |
 |