
Projections et symétries
| Le point N est le projeté du point M sur la droite D parallèlement à la droite D' (prononcer D prime) |
|
Construction:
| Construire le projeté P du point M sur la droite D
parallèlement à la droite D1 .
|
 |
| Pour obtenir ce fameux point P, il faudrait construire la
parallèle à D1 passant par M.
Le point de concours de cette parallèle avec D est le point P: projeté de M sur D parallèlement à D1. |
 |
Une projection particulière: La projection orthogonale
Une projection orthogonale sur une droite D est simplement une projection suivant une direction orthogonale à D
 +
+
Pour construire le projeté orthogonal de M sur une droite D, il suffit de tracer la perpendiculaire à D passant par M (cliquez ici pour voir la méthode au compas ou à l'équerre) , le projeté étant le point de concours des 2 droites.
|
Projection sur D' parallèlement à D Projection orthogonale sur D' |
Le projeté d'un segment sur un droite
parallèlement à une direction donnée est un segment.
Ici: le projeté de [AB] sur la droite D' parallèlement à D est le segment [A'B'] où A' et B' sont les projetés respectifs de A et B. Le projeté du milieu du segment est le milieu du projeté de ce segment. Ici: le projeté de I milieu de [AB] est I' milieu de [A'B'].
|
Distance d'un point à une droite:
| La distance d'un point M à une droite D est la distance MN où N est le projeté orthogonal de M sur D |
Les symétries
| Le point O est le milieu de [AB]. OA=OB
On dit aussi que A et B sont symétriques par rapport au point O. |
 |
| Une figure possède un axe de symétrie lorsque les 2 figures séparées par l'axe se superposent par pliage sur cet axe de symétrie | |
| 2 points A et B sont symétriques orthogonale par rapport à un axe (où une droite) si cette dernière est la médiatrice du segment [AB]. |  |
Connaissant le point A et l'axe D, on peut placer le point B tel que A et B soit symétriques
Le symétrique d'un segment:
|
Les symétries (centrales et axiales) conservent les distances:
donc:
Le symétrique d'un segment est un segment de même longueur.
Le symétrique d'un cercle est un cercle de même rayon.

AB=A'B' |

AB=A'B' |
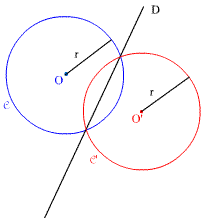
Le symétrique orthogonal du cercle C de centre O de rayon r par rapport à D, est le cercle C' de centre O' symétrique de O et de rayon r |

Le symétrique orthogonal du cercle C de centre O de rayon r par rapport au point I, est le cercle C' de centre O' symétrique de O et de rayon r
|
Les symétries (centrales et axiales) conservent l'alignement des points:
donc, puisqu'elles conservent aussi les distances, elles conservent les milieux:
|
M,N et P sont 3 points alignés, alors, leur symétrique orthogonal respectifs par rapport à D sont 3 points alignés M', N' et P'. |

A, B et C sont 3 points alignés, alors leur symétriques respectifs par rapport à O sont 3 points alignés A' B' et C'. |
|
Le symétrique orthogonal du segment [AB] par rapport à D est le segment [A'B'] (de même longueur). Alors le symétrique de I milieu de [AB] est le milieu de [A'B']. |

Le symétrique du segment [AB] par rapport à O est le segment [A'B'] (de même longueur). Alors le symétrique de I milieu de [AB] est le milieu de [A'B'].
|
Les symétries (centrales et axiales) conservent la mesure des angles
- en particulier, les symétries conservent le parallélisme et la perpendicularité.
- donc, le symétrique (orthogonal ou central) d'un triangle, est un triangle de même nature (en particulier: le symétrique d'un triangle rectangle, isocèle ou équilatéral est un triangle respectivement rectangle, isocèle ou équilatéral)
|
|
|