Les triangles

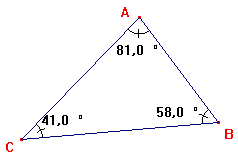
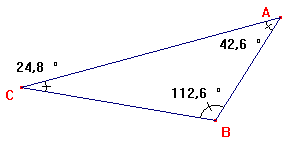
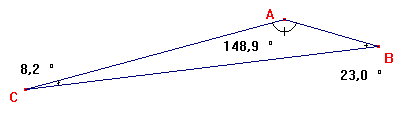
Propriété des angles d'un triangle: La somme des angles d'un triangle est égale à 180°

Des exemples:

81° + 58° +41° = 180° 42,6° + 112,6° + 24,8° = 180° 148,9° + 23° + 8,2° = 180°
Vous pouvez faire les mesures vous-même et additionner vos résultats:

Déplacez le rapporteur avec la souris et faites le pivoter de degré en degré à gauche avec la touche "G" et à droite avec la touche "D".

Pour mieux voir la valeur de la mesure, placez le curseur de la souris où vous voulez zoomer - cliquez sur le bouton de droite (de la souris) et cliquez sur zoom avant

Les droites remarquables d'un triangle:

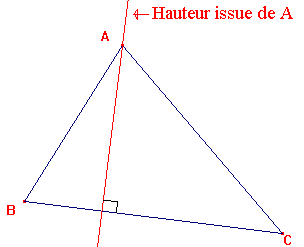
Les hauteurs:

La hauteur issue de A est la droite passant par A et perpendiculaire au côté opposé à A .(c'est à dire le côté [BC] ici).

Souvent une hauteur est assimilé à un segment
On peut ainsi tracer les hauteurs issues des deux autres sommets.

Et que remarque-t-on?

Que les 3 hauteurs sont concourantes: 

elles se coupent en un point appelé l'orthocentre du triangle et noté H

Des exemples d'orthocentre:

remarque importante: lorsqu'un triangle possède un angle obtus, l'orthocentre est à l'extérieur du triangle

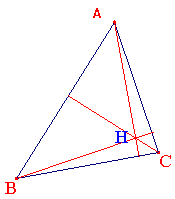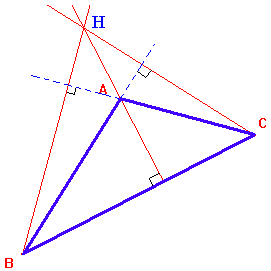les côtés ont dus être prolongés pour tracer les hauteurs

Médiatrices:

La médiatrice d'un segment est la droite qui lui est perpendiculaire en son milieu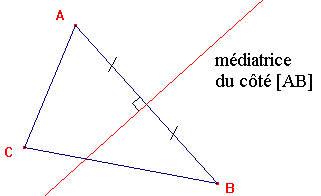
On peut ainsi tracer les médiatrices des 2 autres côtés

Et que remarque-t-on?

Que les 3 médiatrices sont concourantes: 

elles se coupent en un point (noté O) qui le centre du cercle circonscrit au triangle ABC (cercle qui passe par les 3 sommets du triangle)

 

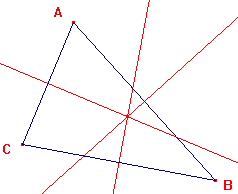
Sur cette figure, vous pouvez déplacer

 

Les médianes:

La médiane issue du sommet B est la droite 
-passant par B 
-et par le milieu du côté opposé à B (c'est à dire [AC])
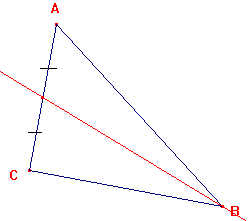On peut ainsi tracer les médianes issues des deux autres côtés.

Et que remarque-t-on?

Que les 3 médianes sont concourantes: 

elles se coupent en un point G appelé centre de gravité du triangle

 

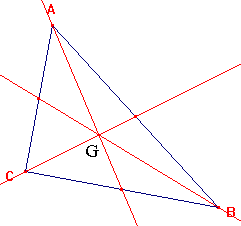Les bissectrices:

La bissectrice de l'angle partage celui-ci en 2 angles égaux
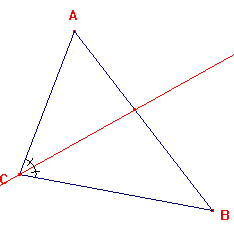On peut ainsi tracer les bissectrices des 2 autres angles.

Et que remarque-t-on?

Que les 3 bissectrices sont concourantes: 

elles se coupent en un point I 

appelé centre du cercle inscrit au triangle (les trois côtés du triangle sont tangents au cercle)

 

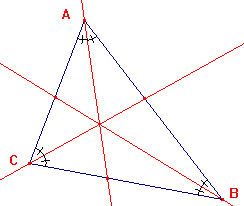
Les  triangles particuliers:

Le triangle isocèle:

Un triangle isocèle est un triangle possédant 2 côtés de même longueur.

propriété: Dans un triangle isocèle, les angles à la base sont égaux

construction:

 

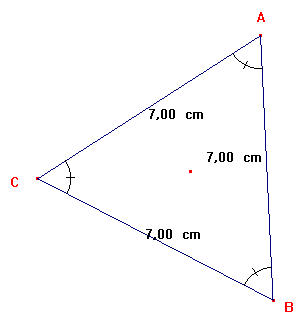
Le triangle équilatéral:

Un triangle équilatéral est un triangle ayant ses 3 côtés de même longueur

propriété: Dans un triangle équilatéral, chaque angle au sommet mesure 60°

construction:

Remarque: la construction d'un triangle équilatérale sert aussi à construire un angle de 60° sans rapporteur.

Le triangle rectangle:

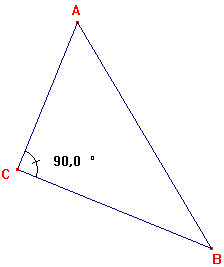
Un triangle rectangle est un triangle possédant un angle droit.

Ici, ABC est un triangle rectangle en C.
Le plus long côté s'appelle l'hypoténuse du triangle rectangle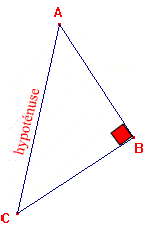
Propriété: Un triangle rectangle est inscriptible dans un cercle dont le diamètre est l'hypoténuse du triangle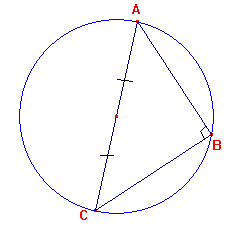